单选题
1、设甲：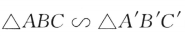
；乙：
.则（）
- A：甲是乙的必要条件但不是充分条件
- B：甲是乙的充分条件但不是必要条件
- C：甲是乙的充要条件
- D：甲既不是乙的充分条件也不是乙的必要条件
答 案：A
解 析：三角形相似不一定全等，但三角形全等一定相似，因此，甲是乙的必要条件但不是充分条件．
2、函数
与y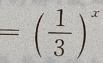
的图像之间的关系是
- A：关于原点对称
- B：关于x轴对称
- C：关于直线 y=1对称
- D：关于y轴对称
答 案：D
解 析：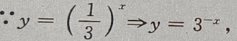
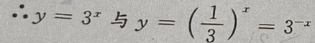关于y轴对称，
3、袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则这2个球都为红球的概率为（）
- A：
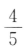
- B：
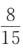
- C：
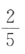
- D：
答 案：C
解 析：两个球都是红球的概率为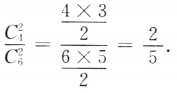
4、不等式|2x-3|≤1的解集为（）
- A：{x|1≤x≤2}
- B：{x|x≤-1或x≥2}
- C：{x|1≤x≤3}
- D：{x|2≤x≤3}
答 案：A
解 析：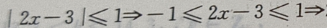
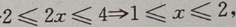故原不等式的解集为{x|1≤x≤2}
主观题
1、设椭圆的中心是坐标原点,长轴在x轴上,离心率
已知点P
到圆上的点的最远距离是
求椭圆的方程
答 案：由题意，设椭圆方程为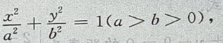
由
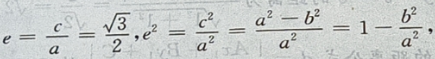
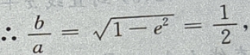设P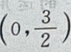
点到椭圆上任一点的距离为 d,
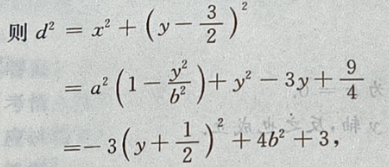
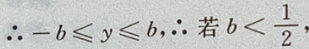则在y=-b时，
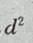最大，即d也最大。
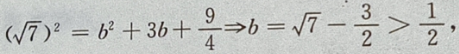
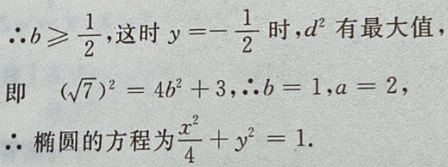
2、设函数f(x)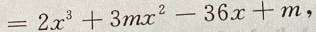
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
答 案：(Ⅰ)由已知得f'=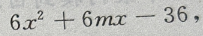
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=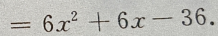
令f'(x)=0，解得
当x<-3时，f'(x)>0;
当-3
3、已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．
答 案：(I）C的焦点为
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
得
设A（x1,y1）.B（x2,y2），则
因此
4、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积
答 案：
填空题
1、设
则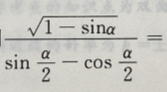
答 案：-1
解 析：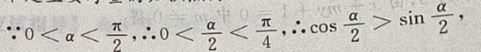
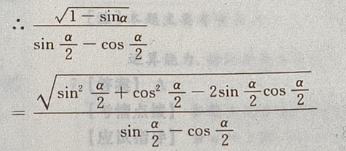
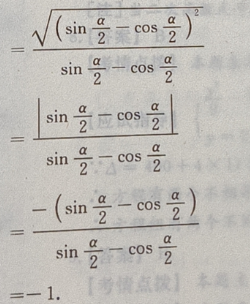
2、函数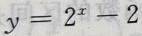
的图像与坐轴的交点共有（）个
答 案：2
解 析：当x=0，
故函数与y轴交于(0,-1)点;令y=0,则有
故函数与工轴交于(1,0)点,因此函数
与坐标轴的交点共有2个
