单选题
1、甲袋内有2个白球3个黑球,乙袋内有3个白球1个黑球,现从两个袋内各摸出1个球,摸出的两个球都是白球的概率是
- A:

- B:
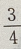
- C:

- D:
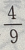
答 案:C
解 析:由已知条件可知此题属于相互独立同时发生的事件,从甲袋内摸到白球的概率为P(A)=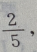 乙袋内摸到白球的概率为
乙袋内摸到白球的概率为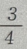 ,所以现从两袋中各提出一个球,摸出的两个都是白球的概率为
,所以现从两袋中各提出一个球,摸出的两个都是白球的概率为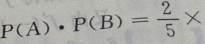
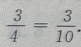
2、若函数f(x)=1+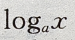 在(0,+∞)上是减函数,则()
在(0,+∞)上是减函数,则()
- A:a>1
- B:a>2
- C:1
- D:0
- D:0
答 案:D
解 析:由已知条件函数f(x)=1+ 3、点(2,4)关于直线y=x的对称点的坐标为()
答 案:A 解 析:点(2,4) 关于直线y=x对称的点为(4,2) 4、设M= 答 案:D 解 析: 主观题 1、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 2、已知三角形的一个内角是 答 案:设三角形三边分别为a,b,c,∠A=60°, 3、已知等差数列 答 案:(Ⅰ)当n=1时,由 4、设椭圆的中心是坐标原点,长轴在x轴上,离心率 答 案:由题意,设椭圆方程为 填空题 1、函数 答 案:2 解 析:当x=0, 2、函数y= 答 案:[1,+∞) 解 析:要是函数y=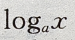 在(0,+∞)上是减函数,及对数函数
在(0,+∞)上是减函数,及对数函数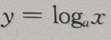 的性质可得底数0
的性质可得底数0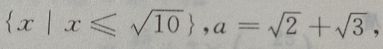 那么()
那么()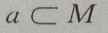
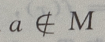
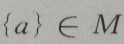
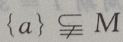
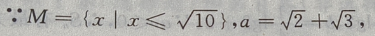 M是集合,a为元素,{a}为集合,元素与集合的关系是
M是集合,a为元素,{a}为集合,元素与集合的关系是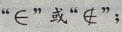 集合与集合的关系是
集合与集合的关系是

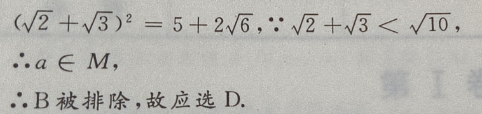
 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
 ,面积是
,面积是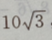 周长是20,求各边的长.
周长是20,求各边的长.
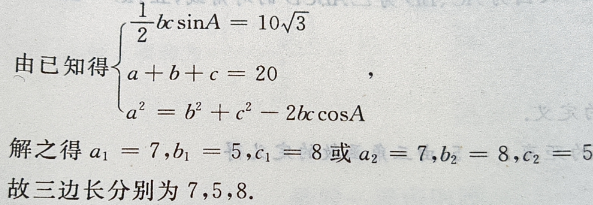
 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项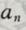 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求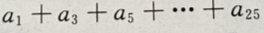 的值
的值
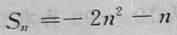 得
得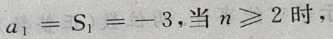
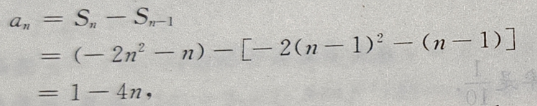
 也满足上式,故
也满足上式,故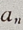 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列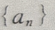 是首项为
是首项为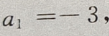 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以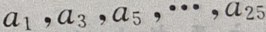 是首项为
是首项为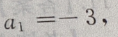 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

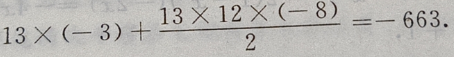
 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
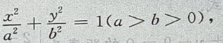 由
由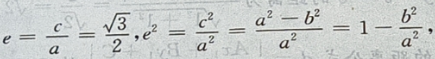
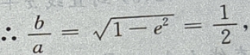 设P
设P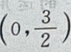 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
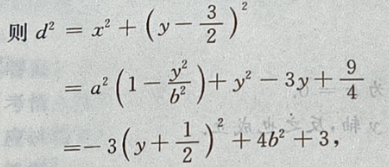
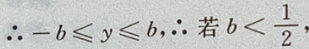 则在y=-b时,
则在y=-b时,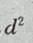 最大,即d也最大。
最大,即d也最大。
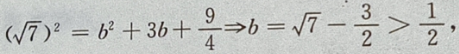

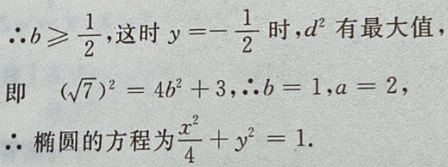
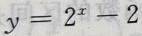 的图像与坐轴的交点共有()个
的图像与坐轴的交点共有()个
 故函数与y轴交于(0,-1)点;令y=0,则有
故函数与y轴交于(0,-1)点;令y=0,则有 故函数与工轴交于(1,0)点,因此函数
故函数与工轴交于(1,0)点,因此函数 与坐标轴的交点共有2个
与坐标轴的交点共有2个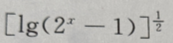 的定义域是()
的定义域是() 有意义,需使
有意义,需使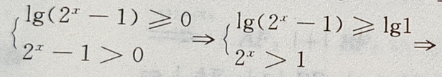
 所以函数的定义域为{x|x≥1}=[1,+∞)
所以函数的定义域为{x|x≥1}=[1,+∞)

