单选题

1、设函数f(x)在（0，1）上可导且在[0，1]上连续，且f'(x)＞0，f(0)＜0，f(1)＞0，则f(x)在（0，1）内（）。

• A：至少有一个零点
• B：有且仅有一个零点
• C：没有零点
• D：零点的个数不能确定

答 案：B

解 析：因为函数f(x)在[0，1]上连续，f(0)＜0，f(1)＞0，故存在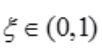，使得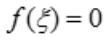，又f'(x)＞0，函数在（0，1）上单调增加，故f(x)在（0，1）内有且仅有一个零点。

2、设y＝5^x，则y'＝（）。

• A：5^x-1
• B：5^x
• C：5^xln5
• D：5^x＋1

答 案：C

解 析：由导数的基本公式可知。

3、微分方程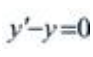的通解为（）。

• A：
• B：
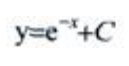
• C：
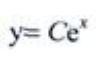
• D：

答 案：C

解 析：所给方程为可分离变量方程，分离变量得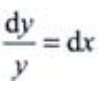，等式两边分别积分得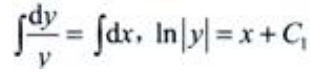，，即。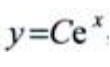

主观题

1、设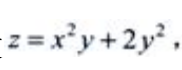求dz。

答 案：解：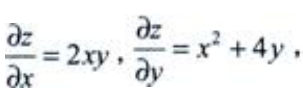

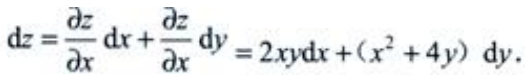
2、设求C的值。

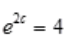答 案：解：则，有，。

3、求函数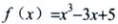的极大值与极小值。

答 案：解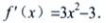：令f′(x)＝0，解得x₁＝－1；x₂＝1又f″(x)＝6x,可知f″(-1)＝－６＜0，f″(1)＝6＞0
故x＝－1为f（x）的极大值点，极大值为7
x＝1为f（x）的极小值点，极小值为3。

填空题

1、极限＝（）。

答 案：

解 析：因为，且分子分母n的最高次方相等，故该极限的值取决于分子分母最高次方的系数比，所以答案为。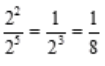

2、设函数z＝f（x，y）可微，（x₀，y₀）为其极值点，则（）。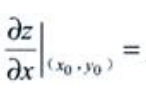

答 案：

解 析：由于z＝f（x，y）可微，则偏导数必定存在，再由二元函数极值的必要条件可知，若点（x₀，y₀）为z＝f（x，y）的极值点，且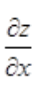，在点（x₀，y₀）处存在，则必有

3、（）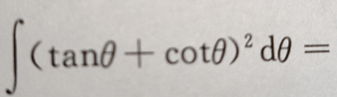

答 案：

解 析：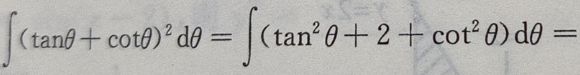

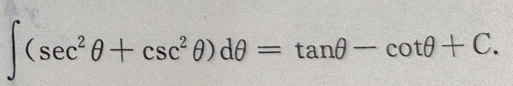
简答题

1、若函数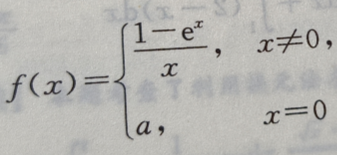在x=0处连续。求a。

答 案：由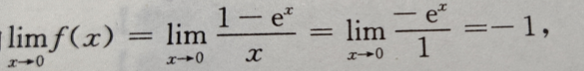 又因f(0)=a,所以当a=-1时，f(x)在x=0连续。